Szelekció - egy lokusz két allél

Az előadáson levezetett egyenlet megadja, hogy mi lesz az allélok gyakorisága a következő generációban. Tehát követhetjük is az allélgyakoriság változását. Az előadáson csak az egyensúlyi pontokat mutattam be, azaz, hogy végtelen idő múlva hol köt ki a populáció. Itt most láthatjuk az időbeli lefolyását a folyamatoknak.

Alkalmazzuk azt helölést, amiben az A₁A₁ genotípus rátermettsége w₁₁=1, az A₁A₂-é w₁₂=1-hs, míg az A₂A₂ genotípusé w₂₂=1-s. Valamint 0<s<1

Domináns előny

A domináns fenotípus előnyt élvez. h=0, s=0,5

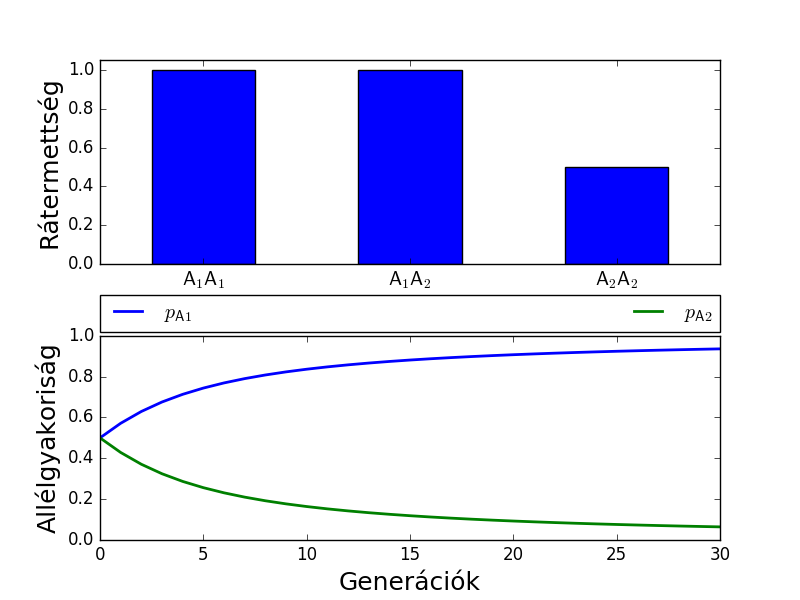
Recesszív előny

A recesszív fenotípus előnyt élvez. h=1, s=0,5. Figyeljük meg, hogy a domináns kevésbé rátermett fenotípus kiszelektálása gyorsabb, mint az előző esetben vizsgált recesszív fenotípus esetében!

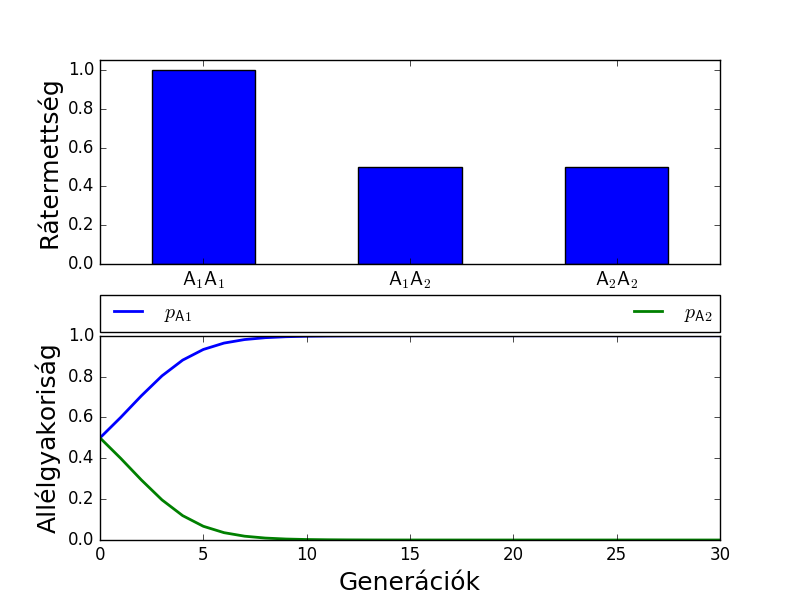
Heterozigóta hátrány

Az A₁A₂ heterozigóta rátermettsége kisebb, mint a két homozigótáé. h=1,5, s=0,5. Ebben az esetben a végkimenet a kezdeti gyakoriságoktól függ. Két példát mutatok, egyikben az A₁ másikban az A₂ terjed el.

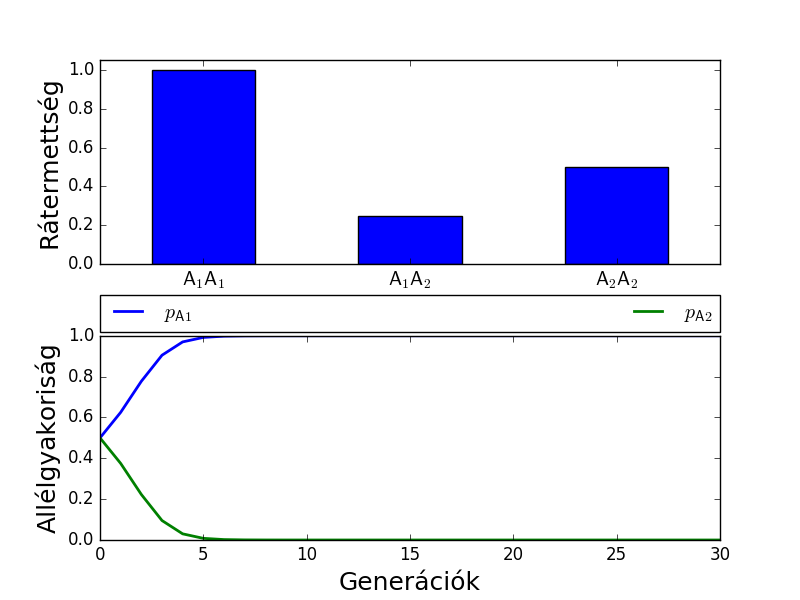
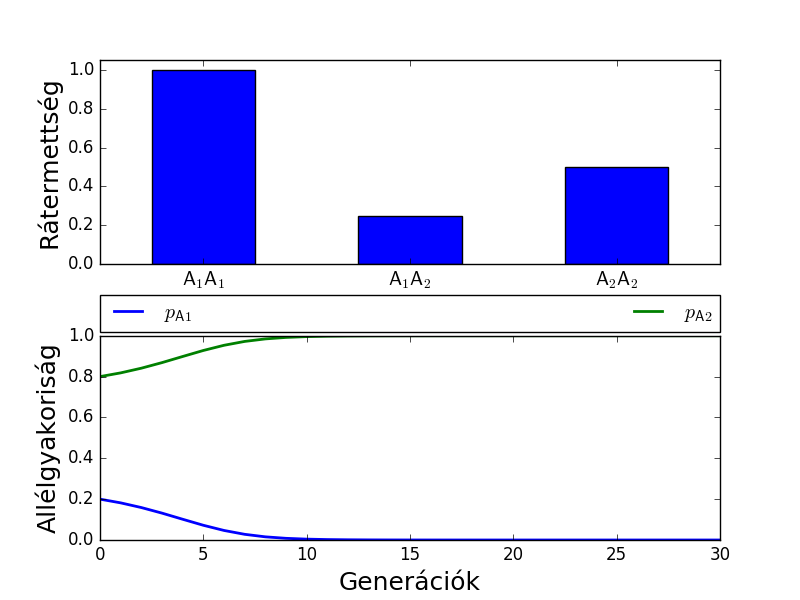
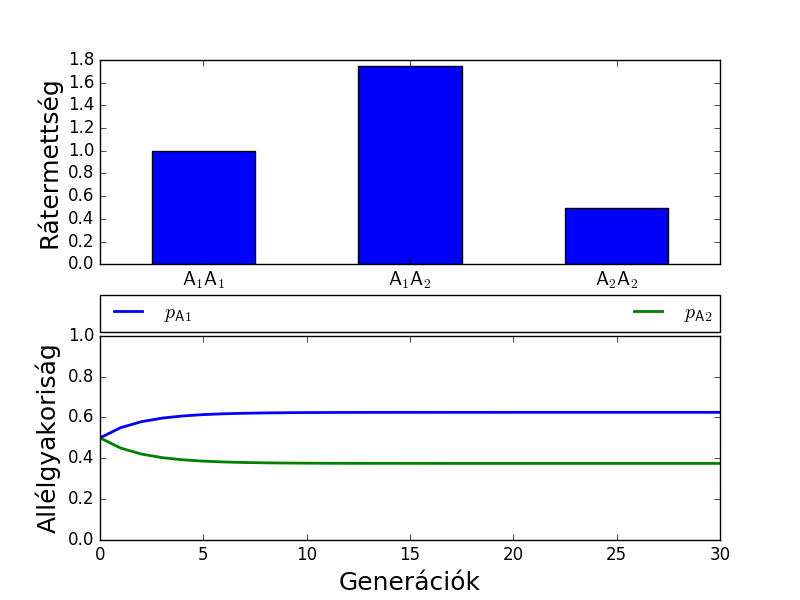
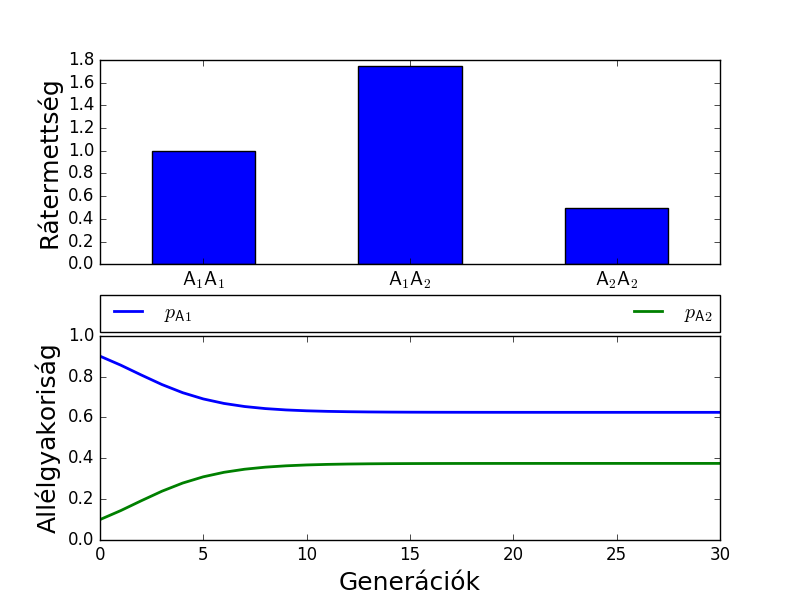
Heterozigóta előny

Az A₁A₂ heterozigóta rátermettsége nagyobb, mint a két homozigótáé. h=-1,5, s=0,5. Mindkét allél megmarad a populációban, védett polimorfizmus alakul ki. Három különböző gyakoriságból kiindulva mutatom, meg, hogy mindig beáll az egyensúly.

A Python program

#############################################################
import matplotlib.pyplot as plt;

Generations = 30;
#Kezdeti gyakoriság itt változtatható
A1_gyakorisag = [0.5];
A2_gyakorisag = [1-A1_gyakorisag[0]];

### w11 = 1
### w12 = 1-hs
### w22 = 1-s
SzelekciosKoefficiens = 0.5;    #s
HeterozigotaHatas = 1;          #h

Figures, Grafok = plt.subplots(2, sharex=False)

for tt in range(Generations):
    A1_gyakorisag.append((A1_gyakorisag[-1]*A1_gyakorisag[-1]+A1_gyakorisag[-1]*A2_gyakorisag[-1]*(1-SzelekciosKoefficiens*HeterozigotaHatas))/(A1_gyakorisag[-1]*A1_gyakorisag[-1]+2*A1_gyakorisag[-1]*A2_gyakorisag[-1]*(1-SzelekciosKoefficiens*HeterozigotaHatas)+A2_gyakorisag[-1]*A2_gyakorisag[-1]*(1-SzelekciosKoefficiens))); #A gyakoriságának meghatározása
    A2_gyakorisag.append(1-A1_gyakorisag[-1])
Grafok[1].plot(range(Generations+1),A1_gyakorisag, label=r'$p_{\mathsf{A}1}$', linewidth=2.0);
Grafok[1].plot(range(Generations+1),A2_gyakorisag, label=r'$p_{\mathsf{A}2}$', linewidth=2.0);


#A fitness értékeket bemutató grafikon
Grafok[0].bar([1,2,3],[1,1-SzelekciosKoefficiens*HeterozigotaHatas,1-SzelekciosKoefficiens],0.5,color='b');
Grafok[0].set_xticks([1.25,2.25,3.25])
Grafok[0].set_xticklabels((r'$\mathsf{A}_1\mathsf{A}_1$',r'$\mathsf{A}_1\mathsf{A}_2$',r'$\mathsf{A}_2\mathsf{A}_2$'), fontsize=14)
Grafok[0].set_ylim([0.0,max(1.05,1-SzelekciosKoefficiens*HeterozigotaHatas+0.05)]);
Grafok[0].set_xlim([0.75,3.75]);
Grafok[0].set_xlabel('Genotípus',fontsize=18)
Grafok[0].set_ylabel('Rátermettség',fontsize=18)

Figures.subplots_adjust(hspace = 0.35)

#Mindenféle beállítása a grafikonnak

Grafok[1].legend(bbox_to_anchor=(0., 1.02, 1., .102), ncol=2, mode="expand",  loc=3, borderaxespad=0.)
#
#Grafok[1].legend(loc=9, borderaxespad=0.)

Grafok[1].set_ylim([0.0,1.0]);
Grafok[1].set_xlabel('Generációk',fontsize=18)
Grafok[1].set_ylabel('Allélgyakoriság',fontsize=18)
plt.show();
#############################################################